Welcome to the SMPBS Web Server (Updated 04/05/2024)
SMPBS (Size Modified Poisson-Boltzmann Solvers) is a comprehensive library of solvers for the size modified Poisson-Boltzmann equation (SMPBE). This library integrates various computational techniques, such as finite element, finite difference, solution decomposition, domain decomposition, and multigrid methods. SMPBS has been recognized in the prestigious the Journal of Computational Chemistry [7]. Additionally, a related platform known as the the SDPBS web server is available, which employs the classic Poisson-Boltzmann model. Together, these resources form a robust toolkit for biochemists, biophysicists, bioengineers, and medical scientists for tackling a wide range of computational chemistry, computational biology, and molecular modeling problems
Applications of the SMPBS Web Server
The SMPBS web server serves as a platform for computing the electrostatic solvation energy of a biomolecule, the binding energy of a biomolecular complex, and the pKa value of a titratable amino acid
To get started, click on one of the links below. Please ensure that Javascript is enabled in your browser to access the SMPBS web server's user-friendly interface.
The SMPBE Model
In the SMPBS web server, the electrostatics of a biomolecule in a symmetric 1:1 ionic solvent is calculated by solving a size modified Poisson-Boltzmann equation (SMPBE) as follows:
\[ \left\{\begin{array}{ll} -\ep\Delta u(\rr)=\displaystyle\frac{10^{10}e_{c}^{2}}{\ez k_{B}T} \displaystyle\sum_{j=1}^{n_p}z_j\delta_{\rr_j}, &\qquad \rr\in D_p, \\ -\es\Delta u(\rr) + \displaystyle\frac{2I_{s}N_{A}e_{c}^{2}}{10^{17}\ez k_{B}T}\sinh(u)=0, &\qquad \rr\in D_s,\\ u(\s^+)=u(\s^-), \quad \displaystyle \es\frac{\partial u(\s^+)}{\partial\nn(\s)}=\ep\frac{\partial u(\s^-)}{\partial\nn(\s)}, &\qquad \s\in\Gamma,\\ u(\s)=g(\s), &\qquad \s\in\partial\Omega, \end{array}\right. \]
where u is an electrostatic potential function in units kBT/ec, Λ is a parameter for characterizing the size effects of ions and water molecules on electrostatics, ∂Ω denotes the boundary of a sufficiently large bounded domain Ω for calculation, Dp, Ds, and Γ denote a solute region hosting the biomolecule, a solvent region, and an interface between the solute and solvent regions, respectively, which satisfy that Ω = Dp ∪ Ds ∪ Γ as illustrated in Figure 1. The other parameters are given in Tables 1,2, and 3.
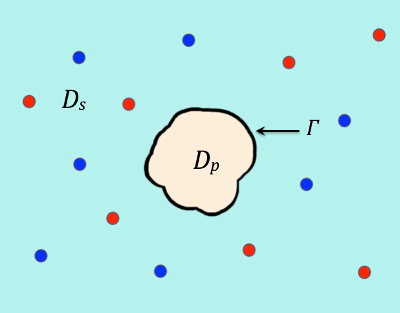
Figure 1. An illustration of a protein region Dp surrounded by solvent region Ds.
Γ denotes the interface and the two species of ions are colored in red and blue.
Additional Notation
| Parameter | Value | Unit (abbr.) | Description |
|---|---|---|---|
| ε0 | 8.854187817 × 10-12 | Farad/meter (F/m) | Permittivity of vacuum |
| ec | 1.602176565 × 10-19 | Coulomb (C) | Elementary charge |
| kB | 1.380648813 × 10-23 | Joule/Kelvin (J/K) | Boltzmann constant |
| NA | 6.0221409 × 1023 | Mole-1 (mol-1) | Avogadro constant |
| Parameter | Default Value | Unit (abbr.) | Description |
|---|---|---|---|
| Λ | 3.11 | Angstrom (Å) | Uniform ionic size parameter |
| εp | 2.0 | Unitless | Biomolecular region dielectric constant |
| εs | 80.0 | Unitless | Solvent region dielectric constant |
| T | 298.15 | Kelvin (K) | Absolute temperature |
| Is | 0.1 | Mole/Liter (mol/l) | Ionic strength |
| Parameter | Description |
|---|---|
| Dp | Protein region |
| Ds | Solvent region |
| Γ | Interface between Dp and Ds |
| Ω | Computational domain satisfying Ω = Dp ∪ Ds ∪ Γ |
| ∂Ω | Boundary of Ω |
| rj | Position of atom j (in angstroms) |
| zj | Charge number of atom j |
| n(s) | Unit outward normal vector of Dp |
| g | Boundary value function |
| δrj | Dirac-delta distribution at atomic position rj |
The SMPBE Solver and Program Package
The SMPBE model is solved numerically in the SMPBS web server by a finite element solver [1] or a finite element and finite difference hybrid solver [4]. Both solvers were developed in Prof. Dexuan Xie's research group by using advanced techniques of solution decomposition, domain decomposition, and multigrid. Their computer programs were written in C++, C, Fortran, and Python based on the state-of-the-art finite element library DOLFIN from the FEniCS Project [2]. Their finite element meshes are generated by our molecular surface-fitted tetrahedral mesh generator, which is an extension of a molecular surface and volumetric mesh generation program package reported in [5] using the molecular triangulation surface mesh generated from either TMSmesh [8] or MSMS [9].
Using the SMPBS Web Server
First, select solvation energy calculation, binding energy calculation, or pKa calculation. Before submitting a job, prepare the PQR file(s) of a biomolecule. This can be done by simply inputting a protein PDB ID and letting the SMPBS web server generate the PQR file. You can also generate a PQR file by downloading a PDB file of the biomolecule from the RCSB Protein Data Bank (PDB), and then converting it to a PQR file by using the web server PDB2PQR. Next, adjust calculation parameters as desired, and submit the job. A typical work flow for a job submission in calculating solvation energy is illustrated in Figure 2.
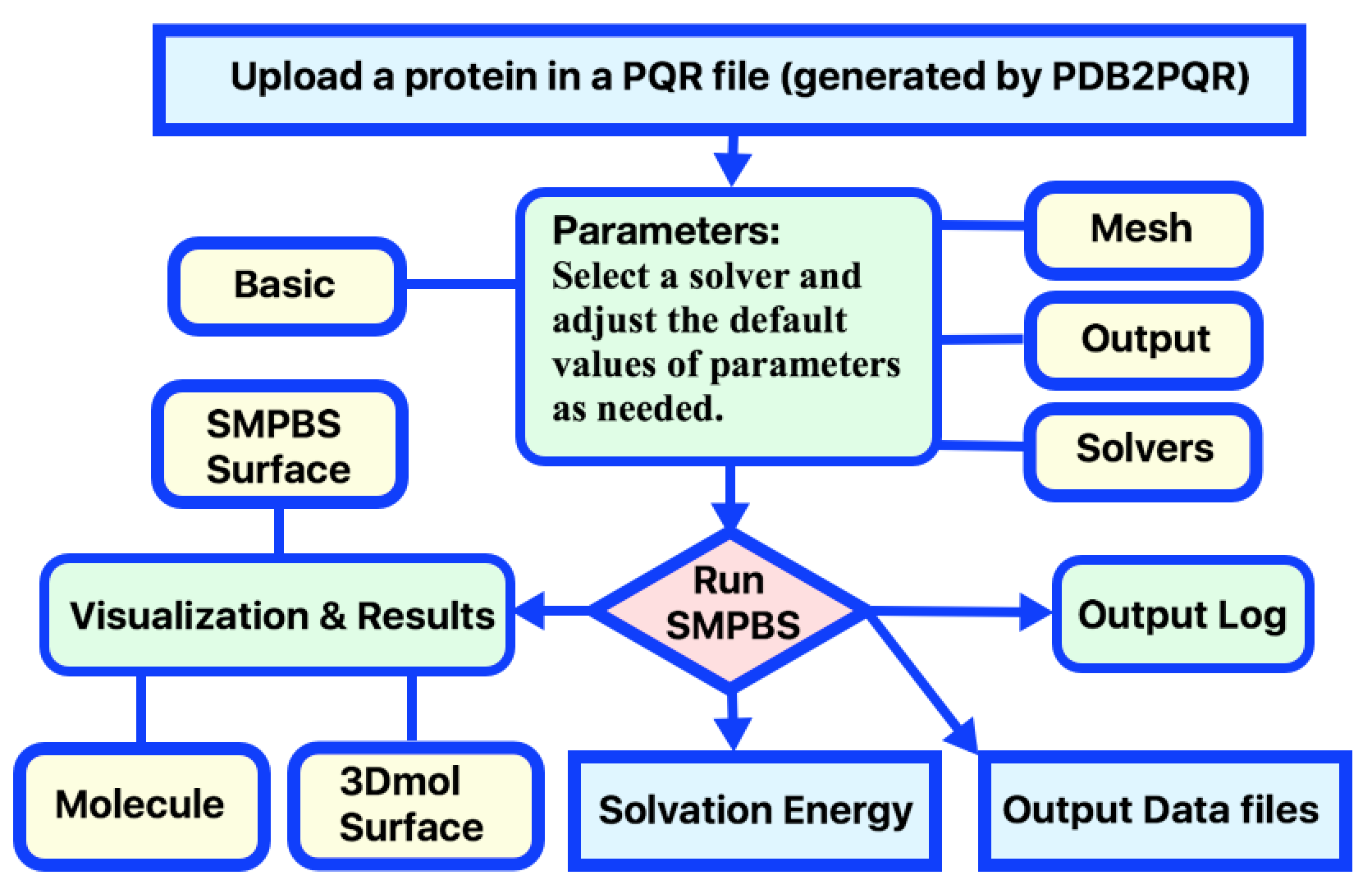
Figure 2. Diagram of of SMPBS Solvation Energy user workflow.
Credits
The SMPBS web server is developed by Professor Dexuan Xie's research group in the Department of Mathematical Sciences and Yang Xie of the Department of Computer Science at University of Wisconsin-Milwaukee (UWM). It is hosted and maintained by the Information Technology Office in the College of Letters and Science at UWM. Development was partially supported by the National Science Foundation, USA, through grant DMS-1226259 and DMS-2153376. Please contact Dexuan Xie via email (dxie@uwm.edu) with any questions regarding the server.
Citing
If this web server is useful in your work, please use the following citation:
- Yang Xie, J. Ying, and D. Xie. SMPBS: Web server for computing biomolecular electrostatics using finite element solvers of size modified Poisson-Boltzmann equation, Journal of Computational Chemistry, 38 (8) (2017) 541-552.
Additional Acknowledgements
- Max Anthony Dreher - implementation of the updated SMPBS web server.
- Jeremy Streich - initial implementation of SDPBS web server and socket programming
- UWM L&S IT Office - internal web development framework and libraries
- Professor David Koes - guidance on integrating 3Dmol.js [6]
- Drs. Yi Jiang and Jinyong Ying - help with SMPBE solver libraries
Update History
- 04/05/2024 - Binding case and pKa temporarily removed
- 09/10/2023 - Add new application for pKa calculation.
- 08/30/2023 - Add references [8] and [9].
- 08/30/2023 - Update the mesh generation package by using TMSmesh or MSMS.
- 08/30/2023 - Remove the solvent-excluded surface (SES) and the solvent-accessible surface (SAS) [3] to simplify the usage.
- 08/30/2023 - Remove the hybrid solver [4] to simplify the usage.
- 08/03/2023 - Updated home page.
- 12/05/2017 - Add reference [7].
- 10/25/2016 - Initial release.
References
- J. Li and D. Xie, An Effective Minimization Protocol for Solving a Size-Modified Poisson-Boltzmann Equation for Biomolecule in Ionic Solvent, International Journal of Numerical Analysis and Modeling, 12 (2015) 286-301. [PDF]
- A. Logg, K.-A. Mardal, and G. N. Wells, eds., Automated Solution of Differential Equations by the Finite Element Method, vol. 84 of Lecture Notes in Computational Science and Engineering, Springer Verlag, 2012. [PDF]
- D. Xu and Y. Zhang. Generating triangulated macromolecular surfaces by Euclidean distance transform. PloS ONE, 4 (12) (2009) e8140s.[PDF]
- J. Ying and D. Xie, A Hybrid Solver of Size modified Poisson-Boltzmann Equation by Domain Decomposition, Finite Element, and Finite Difference, Applied Mathematical Modelling, Vol. 58, pages 166-180, 2018. [PDF]
- Z. Yu, M.J. Holst, Y. Cheng, and J.A. McCammon. Feature-preserving adaptive mesh generation for molecular shape modeling and simulation. Journal of Molecular Graphics and Modelling, 26 (8) (2008) 1370-1380.
- Nicholas Rego and David Koes. 3Dmol.js: molecular visualization with WebGL. Bioinformatics 31 (8) (2015) 1322-1324 doi:10.1093/bioinformatics/btu829. [PDF]
- Yang Xie, J. Ying, and D. Xie. SMPBS: Web server for computing biomolecular electrostatics using finite element solvers of size modified Poisson-Boltzmann equation, Journal of Computational Chemistry, 38 (8) (2017) 541-552. [PDF]
- M. Chen, B. Tu, B. Lu, Triangulated manifold meshing method preserving molecular surface topology, Journal of Molecular Graphics and Modelling 38 (2012) 411-418.
- M. F. Sanner, A. J. Olson, J.-C. Spehner, Reduced surface: an efficient way to compute molecular surfaces, Biopolymers 38 (3) (1996) 305-320
