Features of SMPBS
Comparison of SMPBE with PBE
The SMPBE model is one simple modification of the classic Poisson-Boltzmann equation (PBE) model to reflect the size effects of ions and water molecules on the prediction of ionic concentrations. It is reduced to PBE by setting Λ = 0. For a salt (NaCl) solution, the concentrations CNa and CCl of sodium ions Na+ and chloride ions Cl- are estimated by PBE and SMPBE (in moles per liter) as follows:
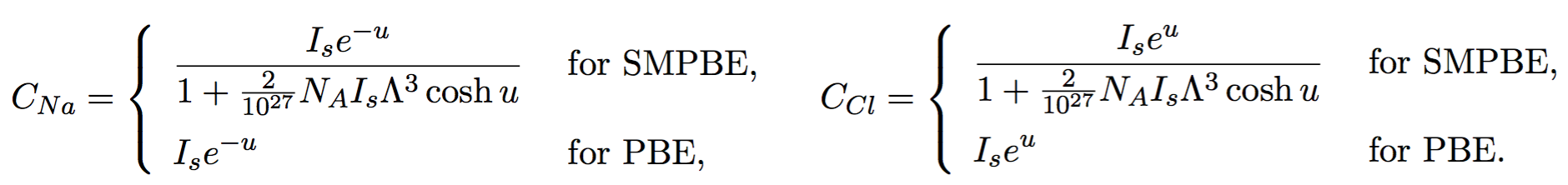
Using the above formulas, we predicted the ionic concentrations in tests on a central charged unit ball and a dipole with two opposite central charges in [1] and [2], respectively, demonstrating that SMPBE can produce physically more reasonable ionic concentrations than PBE. Hence, SMPBE is a more reasonable model than PBE in such an application.
Figure 1 shows that the concentrations CNa and CCl of chloride and sodium ions produced by SMPBE reach a saturation value of 56 around the dipole with positive and negative central charges, respectively [2]. As claimed by the law of electrostatic attraction, both CNa and CCl were found to distribute symmetrically around these two balls.
We also repeated these tests using PBE. Because it treats each ion as a point without any size, PBE produced unreasonably large values of CNa and CCl (greater than 1000) around the two balls.
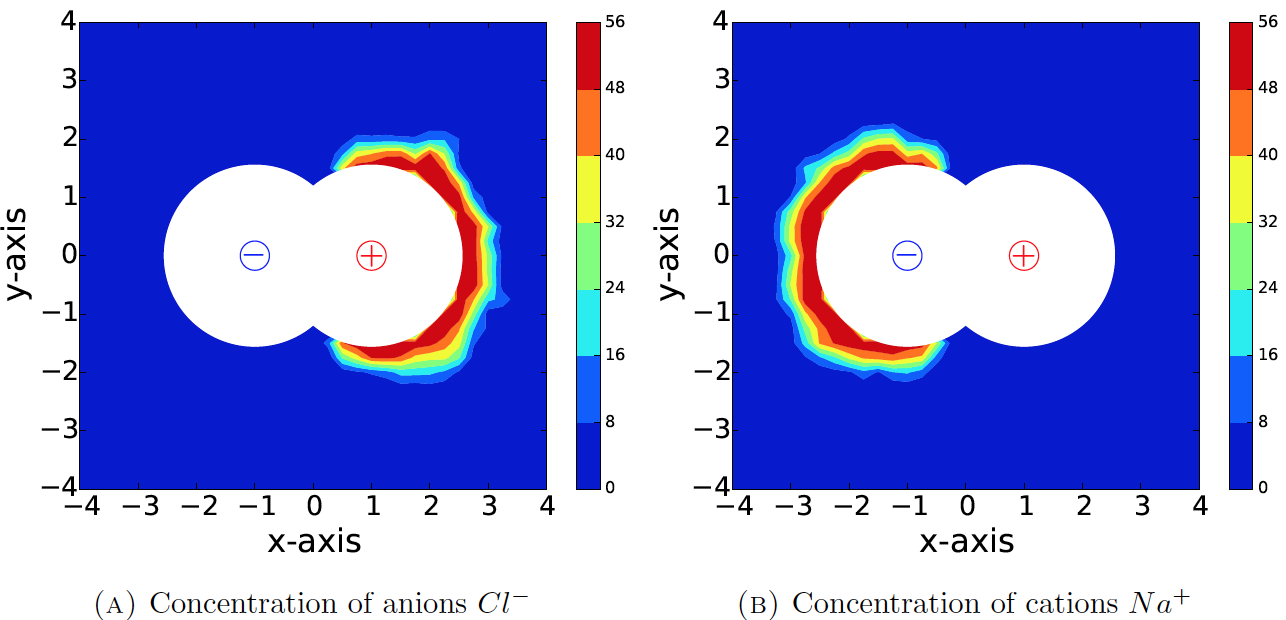
Figure 1. The concentrations of Cl- and Na+ predicted by SMPBE for the dipole consisting of two overlapped balls with two opposite central charges ±3ec. Here, the two balls have the same radius of 1.5 and the centers (±1, 0, 0), Ω = (-12, 12)3, and the boundary value function g = 0.
References
- J. Li and D. Xie, An effective minimization protocol for solving a size-modified Poisson-Boltzmann equation for biomolecule in ionic solvent, International Journal of Numerical Analysis and Modeling, 12 (2015), pp. 286-301.
- J. Ying and D. Xie, A hybrid solver of size modified Poisson-Boltzmann equation by domain decomposition, finite element, and finite difference. arXiv:1610.06173 [math.NA], 2016.
